Table of contents
In our daily used language, we use Grammar, similarly, in computer language, we have a set of rules called grammar on which a language is defined. In this article, we will look into what those Grammars are and how we define and use them.
Exploring the Chomsky Hierarchy of Grammars
Computer languages and grammar studies are pretty cozy with each other, and we can thank Noam Chomsky for that. Chomsky came up with a way to look at grammar mathematically, and it's been a big deal in computational linguistics and computer science. He divided grammars into four types, each with its own complexity and what's needed to process them. This breakdown is super helpful for making programming languages and understanding languages in general.
Type-0 Grammars: Unrestricted Grammar Type-0 grammars are like the Wild West of grammars in Chomsky's world. They don't have any rules holding them back. The languages they create are called recursively enumerable languages. To handle these, you need a Turing machine, which is like the Swiss Army knife of computational models. Anything you can compute, you can express in a Type-0 language. It's the full monty of computing power.
Type-1 Grammars: Context-Sensitive Grammar Next up are Type-1 grammars or context-sensitive ones. These are a bit more reined in than Type-0. They're behind context-sensitive languages, which need a linear bounded automaton to be recognized. Think of it as a Turing machine on a leash, its space directly tied to the input size. These grammars aren't the go-to for programming, but they're key in understanding complex computer languages and even natural languages.
Type-2 Grammars: Context-Free Grammar Then there's Type-2, the context-free grammars. These guys are all about rules that don't care about context. They're recognized by pushdown automata, essentially Turing machines with a memory cap. Most programming languages fall here since they hit that sweet spot of being complex enough for nifty parsing algorithms but not too wild to handle.
Type-3 Grammars: Regular Grammar Finally, at the simpler end, we have Type-3 or regular grammar. These are the most straightforward and limited bunch. They birth regular languages, which a finite state automaton can recognize – basically, the simplest kind of computational model. Regular grammars are the stars in text processing and setting up the groundwork in compilers.
So What is Grammar?
A Grammar can be formally defined as
A Grammar G can be formally described using four tuples a G = ( V, T, S, P) where,
V = set of Variables or Non-Terminal Symbols.
T = Set of Terminal Symbols
S = Start Symbols
P = Production rules for Terminal and non-Terminals
A production rule has the form a -> ß where a and ß are strings on V U T and at least one symbol belongs to V.
Regular Grammar
Regular Grammar can be divided into two types:
- Right Linear Grammar
A Grammar is said to be Right Linear if all productions are of the form
$$A \rightarrow xB$$
$$\ A \rightarrow x$$
$$where \ A,B \in V \ and \ x \in T$$
In simple terms, a Non-terminal symbol (B) lies on the right side of the terminal Symbol.
- Left Linear Grammar
A Grammar is said to be Left Linear if all productions are of the form
$$A \rightarrow Bx$$
$$\ A \rightarrow x$$
$$where \ A,B \in V \ and \ x \in T$$
In simple terms, a Non-terminal symbol (B) lies on the right side of the terminal Symbol.
Derivations from Grammar
The set of all strings that can be derived from a Grammar is said to be the Language Generated from that Grammar.
For Example:
$$G1 = (\{S,A,B\}),\{a.b\},S,\{S \rightarrow AB, A \rightarrow\ a, B \rightarrow\ b \}) \\a$$
Context Free Grammar
In formal language theory, a Context-free language is a language generated by some context-free Grammar.
The set of all Context-free languages is identical to the set of languages accepted by Pushdown Automata.
Context Free Grammar is defined by 4 tuples as G = { V, ∑, S, P } where
V = Set of Variable or Non-Terminal Symbols
∑ = Set of Terminal Symbols
S = Start Symbols
P = Production Rule
$$\text{Context free Grammar has Production Rule of the form } \ A \rightarrow a \ where, a = \{V \ \cup \ ∑ \ \}* \ and \ A \in V$$
Context-Sensitive Grammar
Checking if a certain String Belongs to Grammar or not
Steps
1) Start with the start symbol and choose the closest production that matches to the given string.
2) Replace the variables with their most appropriate production. Repeat the process until the string is generated or until no other productions are left.
Derivation Tree or Parse Tree
A Derivation Tree or Parse Tree is an ordered rooted tree that Graphically represents the semantic information of strings derived from a Context-Free Grammar.
Root Vertex: Must be labeled by the Start Symbol
Vertex: Labelled by Non-Terminal Symbols
Leaves: Labelled by Terminal Symbols or ∈
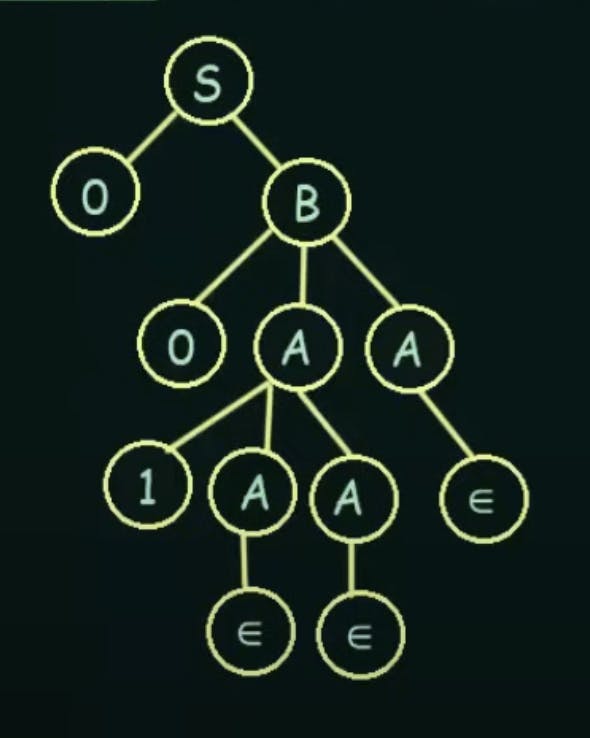
Types of Derivation Tree.
Left Derivation Tree: A left Derivation tree is obtained by applying production to the leftmost variable in each step.
Right Derivation Tree: A Right Derivation Tree is obtained by applying production to the rightmost variable in each step.
Ambiguous Grammar
Grammar is said to be ambiguous if there exist two or more derivatives trees for a string w ( that means two or more left derivation trees)

TL;DR
In this article, we explore the concept of grammar in computer languages, inspired by Noam Chomsky's hierarchy of grammars. Chomsky categorized grammars into four types, each with varying complexity and applications in computational linguistics and computer science:
Type-0 Grammars: Unrestricted grammars with no rules, capable of expressing anything computable.
Type-1 Grammars: Context-sensitive grammars that require linear bounded automata for recognition, useful for understanding complex computer and natural languages.
Type-2 Grammars: Context-free grammars recognized by pushdown automata, commonly used in programming languages.
Type-3 Grammars: Regular grammars recognized by finite state automata, fundamental in text processing and compiler development.
The article also provides formal definitions and explanations for different grammar types, including regular grammar, context-free grammar, and context-sensitive grammar. Additionally, it discusses the concept of derivation trees and ambiguity in grammar.
Conclusion
In summary, grammars play a crucial role in defining the rules of computer languages. Noam Chomsky's hierarchy of grammars categorizes them into four types, each with distinct complexity levels and applications. Understanding these grammar types is essential for programming, computational linguistics, and language processing tasks. Regular grammars are the simplest, while context-sensitive grammars offer a deeper level of complexity, bridging the gap between language theory and practical applications in computer science. Context-free grammars, on the other hand, are widely used in programming languages, making it a critical topic for developers and language designers. Lastly, the article touches on derivation trees and the potential for ambiguity in grammar, highlighting the importance of clarity and precision in language definitions.

